Là môn học bất cứ ai cũng phải trải qua, Toán học không chỉ để tính toán phục vụ cho cuộc sống, mà còn giúp người học khai thác khả năng tư duy logic của mình. Một bài toán tưởng đơn giản nhưng có thể biến đổi bằng nhiều cách khác nhau khiến cho việc học trở nên thú vị hơn bao giờ hết.

Đặc biệt là với những bài toán cho phép tính sai, yêu cầu tìm cách để đưa về dạng đúng, đòi hỏi học trò phải nắm vững kiến thức và áp dụng khéo léo.

Một bài toán thú vị thu hút được nhiều sự quan tâm như sau: 71 dấu chấm tạo thành phép tính (71 + 1)(71 - 1) = 71. Tuy nhiên, phép tính này cho kết quả sai. Bạn cần thêm hoặc bớt 1 dấu chấm trong phép tính này để biến thành đúng.

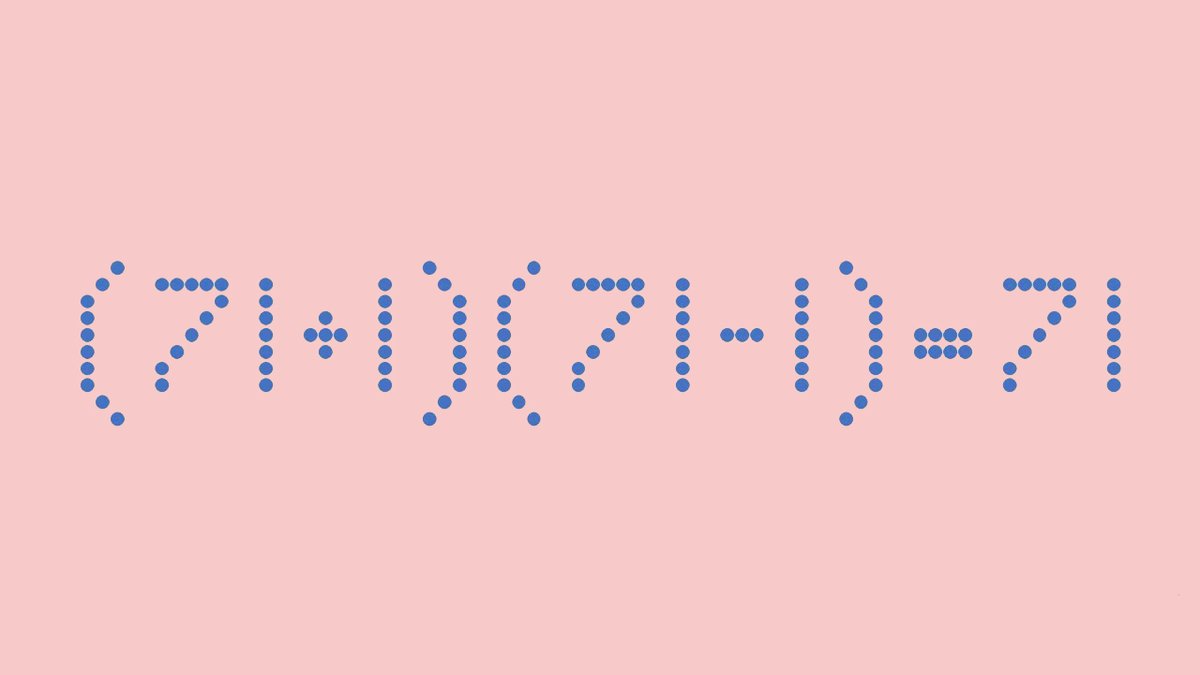
Bài toán yêu cầu biến phép tính sai thành đúng bằng 1 dấu chấm. (Ảnh: Internet)

Nhiều người khi đọc bài toán đã vội lắc đầu ngao ngán vì nhìn khá vô lý, 2 vế hoàn toàn không cân xứng với nhau. Tuy nhiên, điều đó hoàn toàn có thể giải quyết chỉ bằng 1 dấu chấm xanh.

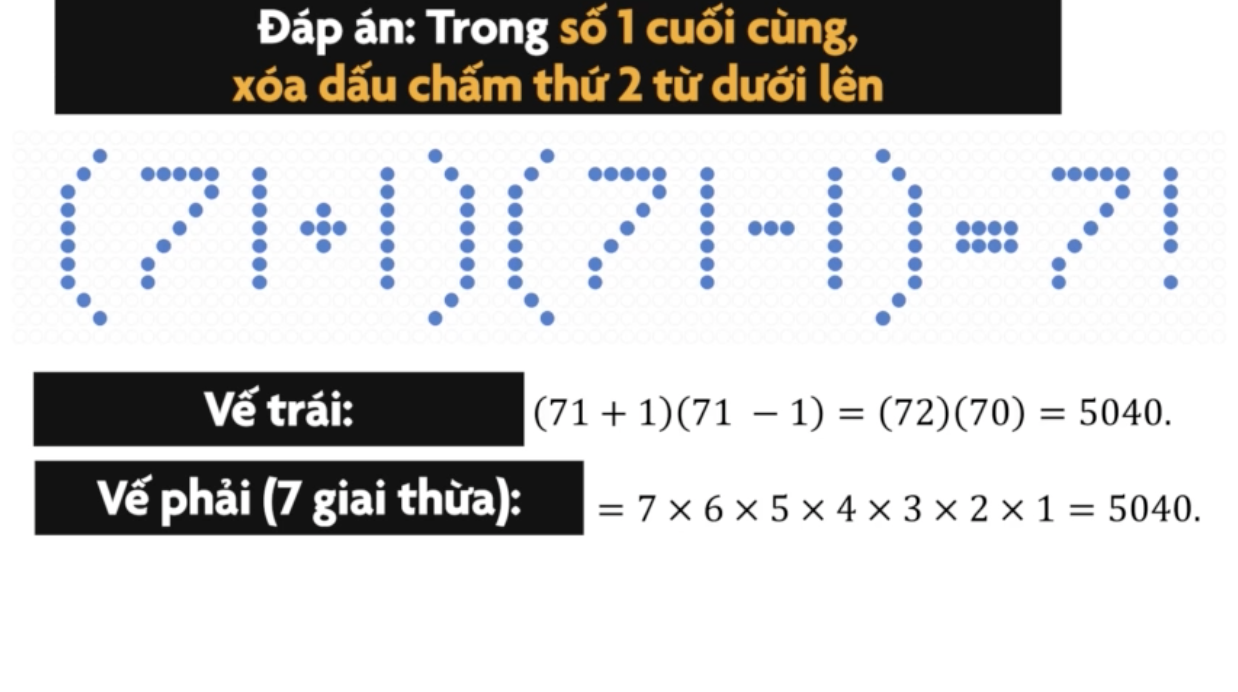
Cụ thể, cách giải phép tính này là: Trong số 1 cuối cùng, xoá dấu chấm thứ 2 từ dưới lên hoặc thêm 1 dấu chấm vào dưới số 1 cuối cùng để tạo ra dấu chấm than (!). Như vậy, vế phải ta có 7! (7 giai thừa).

Xét hai vế ta được:

Vế trái: (71 + 1)(71 - 1) = (72)(70) = 5040.

Vế phải: 7! = 7x6x5x4x3x2x1 = 5040.

Lúc này ta được 2 vế bằng nhau => thoả mãn yêu cầu đề bài.

Đáp án của bài toán hóc búa. (Nguồn: YouTube)

Khi bài toán được giải thích cặn kẽ, nhiều netizen vô cùng bất ngờ vì không ngờ đáp án lại dễ như vậy mà ít người nghĩ đến. Bên cạnh đó, nhiều người cũng thú nhận rằng mình không còn nhớ công thức giai thừa như thế nào vì bình thường ít áp dụng và đã học qua nhiều năm. Vậy mới thấy, để giải được một bài toán cần phải ghi nhớ nhiều công thức cũng như có khả năng tư duy, áp dụng cực nhanh nhạy.